안녕하세요? 이번 글은 'K-평균 클러스터링(K-means clustering)' 알고리즘을 파이썬으로 작성해보도록 하겠습니다. 기존 모듈이 제공하는 함수를 호출하는 것이 아닌, 알고리즘을 하나하나 코드로 작성해가며 개념을 이해하기 위함입니다. 이와 관련하여 저는 최근에 'Machine Learning Algorithms from scratch - Medium'에 소개된 아래 글을 흥미롭게 읽었습니다. 이번 글은 K-평균 클러스터링의 각 단계를 구현할 것이며, 다음 글에서는 K-평균 클러스터링 개선에 관한 나머지 내용을 소개하려고 합니다.
K-means Clustering from Scratch in Python
In this article, we shall be covering the role of unsupervised learning algorithms, their applications, and K-means clustering approach. On…
medium.com
K-평균 알고리즘은 아래 위키백과를 통해 한글화된 설명을 확인하실 수 있습니다.
https://ko.wikipedia.org/wiki/K-%ED%8F%89%EA%B7%A0_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
k-평균 알고리즘 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. k-평균 알고리즘(K-means algorithm)은 주어진 데이터를 k개의 클러스터로 묶는 알고리즘으로, 각 클러스터와 거리 차이의 분산을 최소화하는 방식으로 동작한다. 이
ko.wikipedia.org
위키백과에 소개된 K-평균 표준 알고리즘 절차입니다:

K-평균 알고리즘은 한마디로 '주어진 데이터를 K개의 클러스터로 묶는 것'입니다. 데이터를 K개의 클러스터 중 하나로 지정할 때, 데이터와 각 클러스터들의 중심 간의 유클리드 거리를 계산하여 가장 가까운 클러스터를 찾아 배당하는 방식입니다. 그리고 클러스터들의 중심은 다시 평균으로 이동되며, 클러스터가 변하지 않을 때까지, 즉 수렴할 때까지 반복적인 과정을 거치게 될 것입니다.
자, 그럼 실습에 필요한 모듈들을 호출해 보도록 하겠습니다.
# 모듈 호출
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib.font_manager as fm
import numpy as np
import random as rd이 글에서는 아주 가벼운 양의 데이터를 가지고 K-평균 클러스터링을 다뤄보고자 합니다. 아래 자료는 KOSIS 국가통계포털(http://kosis.kr/)을 통해 제공받은 '국립공원 기본통계: 공원지정 현황'과 '국립공원 기본통계: 탐방객 현황' 자료를 2018년 기준으로 일부 발췌, 정리한 것입니다.
해당 데이터를 판다스 데이터프레임으로 읽어들여 확인해 보겠습니다.
# 국립공원 기본통계 (출처: KOSIS 국가통계포털)
df = pd.read_csv('NLPRK_STA.csv', encoding='cp949')
df.head()
위 데이터는 22개 국립공원에 대한 육지면적(단위: ㎢)과 탐방객수(단위: 명) 통계로 구성되어 있습니다. 우리는 이 2개 특징(features)을 기반으로 하여, 22개 국립공원을 적정 개수의 클러스터로 묶어볼 것입니다. 일단 데이터를 플로팅하여 사상(mapping)을 확인해보도록 하겠습니다.
*플롯에서 한글이 깨지는 경우가 없도록 폰트 검색을 아래와 같이 진행해 봅니다.
저는 제 PC에 'KoPub' 폰트가 존재하는지 여부를 확인해 봤습니다.
fm._rebuild()
[(f.name, f.fname) for f in fm.fontManager.ttflist if 'KoPub' in f.name] # 폰트 검색결과는 아래와 같습니다. 이중 하나를 기본 폰트로 지정하겠습니다.
[('KoPubBatang', 'C:\\Windows\\Fonts\\KoPub Batang Light.ttf'),
('KoPubDotum', 'C:\\Windows\\Fonts\\KoPub Dotum Medium.ttf'),
('KoPubDotum', 'C:\\Windows\\Fonts\\KoPub Dotum Bold.ttf'),
('KoPubBatang', 'C:\\Windows\\Fonts\\KoPub Batang Bold.ttf'),
('KoPubBatang', 'C:\\Windows\\Fonts\\KoPub Batang Medium.ttf'),
('KoPubDotum', 'C:\\Windows\\Fonts\\KoPub Dotum Light.ttf')]
플롯을 위한 스타일, 폰트, 폰트 축척을 지정하였습니다.
sns.set(style='whitegrid', font='KoPubDotum', font_scale=1.2) # Seaborn 설정데이터 프레임에서 국립공원 육지면적, 탐방객수 컬럼만 선택해서 X로 정의해 줍니다.
여기서 X는 (22, 2)의 2차원 배열이며 집합 개수 22는 m으로, 특징 개수 2는 n으로 선언해 줍니다.
# 국립공원 육지면적, 탐방객수
X = df.iloc[:, [1, 2]].values # shape=(22, 2)
m=X.shape[0] # 집합 개수 (m=22)
n=X.shape[1] # 특징 개수 (n=2)x축은 '육지면적', y축은 '탐방객수'로 설정한 상태에서 22개 국립공원을 사상(mapping)해 봅니다.
plt.scatter(X[:,0],X[:,1],c='black',label='국립공원')
plt.xlabel('육지면적 (㎢)')
plt.ylabel('탐방객수 (명)')
plt.legend()
plt.title('국립공원')
plt.show()
탐방객수가 가장 많은 곳은 '한려해상국립공원'이고, 가장 적은 곳은 '월출산국립공원'입니다.
반대로 육지면적이 가장 넓은 곳은 '지리산국립공원'이고, 가장 좁은 곳은 '태안해안국립공원'입니다.
위 그래프 영역을 임의로 나눠 클러스터를 정의하고, 각 데이터를 강제 배당할 수도 있습니다. 다소 주관적이겠죠?!
K-평균 알고리즘으로 구현한다면 클러스터 개수 K와, 임의의 K개 좌표를 각 클러스터의 중심 초기값으로 정해야 합니다.
일단, 클러스터 개수는 3개로 설정하겠습니다.
K=3 # 클러스터 개수반복 횟수는 100회로 설정했습니다. 수렴 여부를 확인한다면, 이 조건은 생략될 수 있겠습니다.
n_iter=100 # 반복 횟수클러스터 중심 데이터 값을 저장하기 위한 (2, 0)의 2차원 배열을 생성해 줍니다. 현재는 비어있는 상태입니다.
Centroids=np.array([]).reshape(n,0) # 클러스터 중심 초기화
Centroids # shape=(2, 0)배열 연산을 위해 우리는 파이썬 라이브러리 중 'NumPy(넘파이)'의 도움을 구할 것입니다.
넘파이를 통해 우리는 다차원 배열의 연산을 쉽게 수행할 수 있습니다. 관련 그림은 아래와 같습니다:
그림 출처: https://www.oreilly.com/library/view/elegant-scipy/9781491922927/ch01.html

파이썬에 익숙치 않은 분들을 위한 몇가지 예시 코드를 제시해 봅니다.
첫번째는 0부터 2까지 수를 순차적으로 출력하는 반복문의 예시입니다.
# 반복문 예시
for i in range(3):
print(i) # 0 1 2두번째는 두 수 사이의 난수(정수)를 생성하는 rand.randint()의 예시입니다. 아래는 0, 1, 2 중 하나의 난수가 생성됩니다.
# 두 수 사이의 난수(정수) 생성 예시
rd.randint(0,2) # 0과 2 사이 난수(정수) 생성: 0, 1, 2위의 코드 예시를 활용해서 K개 클러스터 중심 초기값을 설정해 봅니다.
아래 구문에서 반복문은 클러스터 개수만큼 반복(K=3이므로 3회)됩니다. 그리고 집합의 색인에 해당하는 0과 21 사이의 난수(정수)가 3개 생성될 것입니다. 2차원 배열 X 중 해당 색인에 해당하는 벡터 값들은 클러스터 중심으로 설정되어 2차원 배열 Centroids에 저장될 것입니다. *코드에서 np_c[a, b]는 배열을 옆으로 붙이는 방식입니다.
for i in range(K): # 0, 1, 2
rand=rd.randint(0,m-1) # 0과 21 사이 난수 생성
Centroids=np.c_[Centroids,X[rand]] # 클러스터 중심(열) 추가
Centroids # K개 클러스터 중심 초기값. shape=(2, 3)여기서 임의로 선택된 3개 클러스터 중심 초기값은 아래와 같습니다. 행은 특징 2개를, 열은 3개 클러스터를 지시하므로 차원은 (2, 3)이 됩니다. 1회의 반복처리가 진행되고 나면, Centroids 배열은 각 클러스터의 평균값으로 배당될 것입니다.
array([[7.625600e+01, 2.910230e+02, 4.830220e+02],
[6.729010e+05, 1.987762e+06, 3.308833e+06]])우리가 얻게 될 출력값, 즉 각 데이터에 대한 클러스터 배당 값은 Output이라는 딕셔너리로 선언해 둡니다.
Output={} # 출력값 초기화(딕셔너리)딕셔너리는 키(key)와 그에 상응하는 값(value)으로 존재합니다. 키는 1, 2, 3 클러스터가 될 것이며 값은 각 클러스터로 할당된 데이터 배열이 될 것입니다. *딕셔너리의 '키'와 '값'의 구조는 아래 그림을 참조하시면 됩니다.
그림 출처: https://developers.google.com/edu/python/dict-files?hl=ko

이제 할 일은 각 데이터와 클러스터 중심 간의 '유클리드 거리'를 계산하는 것입니다.
이를 위해 계산값을 저장할 배열을 아래와 같이 (22, 0)크기로 초기화 선언해 줍니다.
# 유클리드 거리 초기화
EuclidianDistance=np.array([]).reshape(m,0)
EuclidianDistance # shape=(22, 0)이제 데이터 X와 클러스터 중심 Centroids 간의 유클리드 거리를 계산할 것입니다.
여기서 한가지 고려사항이 존재합니다. 일단 X는 (22, 2)의 2차원 배열이고,
array([[4.830220e+02, 3.308833e+06],
[1.365500e+02, 2.887634e+06],
[6.533500e+01, 1.817602e+06],
[1.271880e+02, 6.439653e+06],
[3.982370e+02, 3.241484e+06],
[2.747660e+02, 1.244854e+06],
[1.533320e+02, 8.918170e+05],
[8.070800e+01, 1.948616e+06],
[7.625600e+01, 6.729010e+05],
[2.294300e+02, 1.501306e+06],
[3.263480e+02, 1.399119e+06],
[1.055950e+02, 1.155063e+06],
[2.422300e+01, 1.049974e+06],
[2.910230e+02, 1.987762e+06],
[7.692200e+01, 5.518508e+06],
[1.756680e+02, 7.383680e+05],
[2.875710e+02, 1.014793e+06],
[3.220110e+02, 1.193986e+06],
[1.367070e+02, 1.579089e+06],
[5.622000e+01, 4.089300e+05],
[7.542500e+01, 3.143779e+06],
[7.005200e+01, 6.800680e+05]])Centroids는 각 K에 대해 선택될 텐데 아래와 같이 (2,)의 1차원 배열에 해당됩니다.
즉, 행렬과 벡터 간의 연산을 필요로 합니다. 이것을 프로그래밍으로 어떻게 구현해야 할까요?!
Centroids[:,0] # shape=(2,)array([7.62560e+01, 6.72901e+05])결론적으로는 넘파이의 도움을 받으면 됩니다. 넘파이의 '브로드캐스트(broadcast)' 기능을 통해 형상이 다른 배열끼리도 계산이 가능하기 때문입니다. 예컨데 (22, 2)의 행렬 X에서 (2,)의 Centroids[:,0]을 차감하면, Centroids[:,0]는 (22, 2) 행렬로 확대된 후 연산이 진행됩니다. 계산상 이유로 유클리드 거리의 루트는 생략되었으며, 결과값은 (22,)의 벡터로 도출됩니다.
# 넘파이 브로드캐스트(broadcast): 형상이 다른 배열끼리도 계산 가능
# (22, 2) 행렬 A에서 (2,) 벡터 값을 차감하면, 벡터 값은 (22, 2) 행렬로 확대된 후 연산
tempDist = np.sum((X-Centroids[:,0])**2,axis=1)
tempDist # shape=(22,)array([6.94813767e+12, 4.90504226e+12, 1.31034038e+12, 3.32554286e+13,
6.59761873e+12, 3.27130274e+11, 4.79242210e+10, 1.62744876e+12,
0.00000000e+00, 6.86254867e+11, 5.27392646e+11, 2.32480195e+11,
1.42184050e+11, 1.72885950e+12, 2.34799072e+13, 4.28593797e+09,
1.16890184e+11, 2.71529638e+11, 8.21176695e+11, 6.96806892e+10,
6.10523809e+12, 5.13659275e+07])*넘파이의 브로드캐스트 기능은 다음 그림이 참고가 되겠습니다.
그림 출처: https://www.researchgate.net/figure/Broadcasting-in-NumPy_fig1_326377197
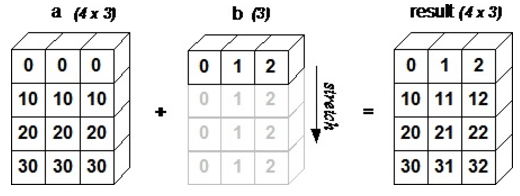
그리고 EuclidianDistance 배열은 (22, 0)에서 (22, 1) 크기로 갱신됩니다.
np.c_[EuclidianDistance,tempDist] # (22, 0) 행렬에 (22,) 옆으로 붙이기array([[6.94813767e+12],
[4.90504226e+12],
[1.31034038e+12],
[3.32554286e+13],
[6.59761873e+12],
[3.27130274e+11],
[4.79242210e+10],
[1.62744876e+12],
[0.00000000e+00],
[6.86254867e+11],
[5.27392646e+11],
[2.32480195e+11],
[1.42184050e+11],
[1.72885950e+12],
[2.34799072e+13],
[4.28593797e+09],
[1.16890184e+11],
[2.71529638e+11],
[8.21176695e+11],
[6.96806892e+10],
[6.10523809e+12],
[5.13659275e+07]])클러스터 개수 K 만큼 반복되면, EuclidianDistance 배열은 (22, 3) 크기가 됩니다.
for k in range(K): # 0, 1, 2
tempDist=np.sum((X-Centroids[:,k])**2,axis=1)
EuclidianDistance=np.c_[EuclidianDistance,tempDist]
EuclidianDistance # shape=(22, 3)각 데이터에 대하여 첫번째, 두번째, 세번째 컬럼은 k번째 클러스터 중심 간의 거리 분산에 해당됩니다.
array([[6.94813767e+12, 1.74522862e+12, 0.00000000e+00],
[4.90504226e+12, 8.09769640e+11, 1.77408718e+11],
[1.31034038e+12, 2.89544765e+10, 2.22377007e+12],
[3.32554286e+13, 1.98193335e+13, 9.80203400e+12],
[6.59761873e+12, 1.57181886e+12, 4.53589499e+09],
[3.27130274e+11, 5.51912297e+11, 4.26000936e+12],
[4.79242210e+10, 1.20109546e+12, 5.84196645e+12],
[1.62744876e+12, 1.53245355e+09, 1.85019045e+12],
[0.00000000e+00, 1.72885950e+12, 6.94813767e+12],
[6.86254867e+11, 2.36639444e+11, 3.26715392e+12],
[5.27392646e+11, 3.46500583e+11, 3.64700759e+12],
[2.32480195e+11, 6.93387659e+11, 4.63872536e+12],
[1.42184050e+11, 8.79446404e+11, 5.10244419e+12],
[1.72885950e+12, 0.00000000e+00, 1.74522862e+12],
[2.34799072e+13, 1.24661674e+13, 4.88266377e+12],
[4.28593797e+09, 1.56098538e+12, 6.60729041e+12],
[1.16890184e+11, 9.46668675e+11, 5.26261956e+12],
[2.71529638e+11, 6.30080339e+11, 4.47257786e+12],
[8.21176695e+11, 1.67013645e+11, 2.99201443e+12],
[6.96806892e+10, 2.49271054e+12, 8.40943759e+12],
[6.10523809e+12, 1.33637535e+12, 2.72429891e+10],
[5.13659275e+07, 1.71006365e+12, 6.91040560e+12]])유클리드 거리가 최소가 되는 색인은 np.argmin() 함수를 통해 계산 가능합니다.
# 유클리드 거리가 최소가 되는 색인
np.argmin(EuclidianDistance,axis=1)결과는 다음과 같습니다. 클러스터는 0, 1, 2보다는 1, 2, 3으로 정해 보겠습니다.
array([2, 2, 1, 2, 2, 0, 0, 1, 0, 1, 1, 0, 0, 1, 2, 0, 0, 0, 1, 0, 2, 0],
dtype=int64)이렇게 계산된 클러스터 정보는 C 벡터로 저장합니다.
# K 클러스터 저장
C=np.argmin(EuclidianDistance,axis=1)+1
C # shape=(22,)array([3, 3, 2, 3, 3, 1, 1, 2, 1, 2, 2, 1, 1, 2, 3, 1, 1, 1, 2, 1, 3, 1],
dtype=int64)자, 이제 클러스터가 배당되었습니다. 이제 반복문이 등장해야겠죠?!
출력값의 임시 저장을 위한 딕셔너리 Y를 생성합니다.
Y={} # 출력값 임시 딕셔너리Y에서 키 값은 1, 2, 3이고 각 키마다 (2,0) 크기의 배열이 정의됩니다.
for k in range(K): # 0, 1, 2
Y[k+1]=np.array([]).reshape(2,0) # 특징 개수
Y{1: array([], shape=(2, 0), dtype=float64),
2: array([], shape=(2, 0), dtype=float64),
3: array([], shape=(2, 0), dtype=float64)}C[0]은 0번째 데이터가 현재 할당된 클러스터 번호입니다. 따라서 1, 2, 3 중 하나의 값을 가지고 있습니다.
Y는 해당 키 값을 가지고 있는 배열에 0번째 데이터의 특징 값을 옆으로 붙여넣으며 업데이트할 것입니다.
# 출력값 임시 딕셔너리 갱신
Y[C[0]]=np.c_[Y[C[0]],X[0]] # C[0] 키 값에 대한 재귀적 갱신
Y[C[0]]array([[4.830220e+02],
[3.308833e+06]])이 과정을 데이터 개수만큼 반복합니다.
# 출력값 임시 딕셔너리: 키 값에 대한 재귀적 갱신
for i in range(m): # m=22
Y[C[i]]=np.c_[Y[C[i]],X[i]]
Y결과는 아래와 같습니다. 각각의 클러스터에 대해 데이터들이 위치한 것을 확인하실 수 있습니다.
우리 머릿 속에는 현재 벡터와 행렬로 된 텐서(tensor)가 코딩을 타고 흐르는(flow) 중일 것입니다.
{1: array([[2.747660e+02, 1.533320e+02, 7.625600e+01, 1.055950e+02,
2.422300e+01, 1.756680e+02, 2.875710e+02, 3.220110e+02,
5.622000e+01, 7.005200e+01],
[1.244854e+06, 8.918170e+05, 6.729010e+05, 1.155063e+06,
1.049974e+06, 7.383680e+05, 1.014793e+06, 1.193986e+06,
4.089300e+05, 6.800680e+05]]),
2: array([[6.533500e+01, 8.070800e+01, 2.294300e+02, 3.263480e+02,
2.910230e+02, 1.367070e+02],
[1.817602e+06, 1.948616e+06, 1.501306e+06, 1.399119e+06,
1.987762e+06, 1.579089e+06]]),
3: array([[4.830220e+02, 4.830220e+02, 1.365500e+02, 1.271880e+02,
3.982370e+02, 7.692200e+01, 7.542500e+01],
[3.308833e+06, 3.308833e+06, 2.887634e+06, 6.439653e+06,
3.241484e+06, 5.518508e+06, 3.143779e+06]])}두번째는 계산상 이유로 Y를 전치행렬(transposed matrix)로 업데이트 시켜줍니다.
넘파이 배열에서 아래와 같이 .T를 붙여주시면 쉽게 행과 열을 교환할 수 있습니다.
Y[1] # shape=(10, 2)array([[2.747660e+02, 1.244854e+06],
[1.533320e+02, 8.918170e+05],
[7.625600e+01, 6.729010e+05],
[1.055950e+02, 1.155063e+06],
[2.422300e+01, 1.049974e+06],
[1.756680e+02, 7.383680e+05],
[2.875710e+02, 1.014793e+06],
[3.220110e+02, 1.193986e+06],
[5.622000e+01, 4.089300e+05],
[7.005200e+01, 6.800680e+05]])Y[1].T # 전치행렬: shape=(2, 10)array([[2.747660e+02, 1.533320e+02, 7.625600e+01, 1.055950e+02,
2.422300e+01, 1.756680e+02, 2.875710e+02, 3.220110e+02,
5.622000e+01, 7.005200e+01],
[1.244854e+06, 8.918170e+05, 6.729010e+05, 1.155063e+06,
1.049974e+06, 7.383680e+05, 1.014793e+06, 1.193986e+06,
4.089300e+05, 6.800680e+05]])반복문으로 각각의 'k' 키 값에 대한 행렬의 위치를 바꿔줍니다.
# 출력값 임시 디렉터리: 전치행렬
for k in range(K): # 0, 1, 2
Y[k+1]=Y[k+1].T
Y{1: array([[2.747660e+02, 1.244854e+06],
[1.533320e+02, 8.918170e+05],
[7.625600e+01, 6.729010e+05],
[1.055950e+02, 1.155063e+06],
[2.422300e+01, 1.049974e+06],
[1.756680e+02, 7.383680e+05],
[2.875710e+02, 1.014793e+06],
[3.220110e+02, 1.193986e+06],
[5.622000e+01, 4.089300e+05],
[7.005200e+01, 6.800680e+05]]), 2: array([[6.533500e+01, 1.817602e+06],
[8.070800e+01, 1.948616e+06],
[2.294300e+02, 1.501306e+06],
[3.263480e+02, 1.399119e+06],
[2.910230e+02, 1.987762e+06],
[1.367070e+02, 1.579089e+06]]), 3: array([[4.830220e+02, 3.308833e+06],
[4.830220e+02, 3.308833e+06],
[1.365500e+02, 2.887634e+06],
[1.271880e+02, 6.439653e+06],
[3.982370e+02, 3.241484e+06],
[7.692200e+01, 5.518508e+06],
[7.542500e+01, 3.143779e+06]])}각 클러스터의 육지면적 값과 탐방객수 값을 axis 0 축으로 평균화 해줍니다.
그리고 이 값은 Centroids 배열에서 해당 클러스터 특징 값으로 갱신됩니다.
for k in range(K): # 0, 1, 2
Centroids[:,k]=np.mean(Y[k+1],axis=0)
Centroidsarray([[1.54569400e+02, 1.88258500e+02, 2.54338000e+02],
[9.05075400e+05, 1.70558233e+06, 3.97838914e+06]])지금까지 나눠서 본 코드를 하나의 반복문으로 정렬해 보면 다음과 같습니다.
for i in range(n_iter): # n_iter 반복 횟수
# 유클리드 거리가 최소가 되는 K 클러스터 할당
EuclidianDistance=np.array([]).reshape(m,0)
for k in range(K):
tempDist=np.sum((X-Centroids[:,k])**2,axis=1) # shape=(22,)
EuclidianDistance=np.c_[EuclidianDistance,tempDist] # shape=(22, 3)
C=np.argmin(EuclidianDistance,axis=1)+1 # shape=(22,)
# K 클러스터 갱신
Y={}
for k in range(K):
Y[k+1]=np.array([]).reshape(2,0) # Y 딕셔너리 키, 값 할당
for i in range(m):
Y[C[i]]=np.c_[Y[C[i]],X[i]] # Y 딕셔너리 키(K클러스터), 값(육지면적, 탐방객수) 할당
for k in range(K):
Y[k+1]=Y[k+1].T # 전치행렬
for k in range(K):
Centroids[:,k]=np.mean(Y[k+1],axis=0) # K 클러스터 중심 갱신
Output=Y결과를 확인해 볼까요?! 그래프로 그려보면 다음과 같습니다.
# K-평균 클러스터링 결과 가시화
color=['red','blue','green']
labels=['cluster1','cluster2','cluster3']
for k in range(K):
plt.scatter(Output[k+1][:,0],Output[k+1][:,1],c=color[k],label=labels[k])
plt.scatter(Centroids[0,:],Centroids[1,:],s=300,c='yellow',label='Centroids')
plt.xlabel('육지면적 (㎢)')
plt.ylabel('탐방객수 (명)')
plt.legend()
plt.show()
cluster1: 가야산, 소백산, 속리산, 월악산, 월출산, 주왕산, 치악산, 태백산, 태안해안, 한라산
cluster2: 경주, 계룡산, 내장산, 다도해해상, 덕유산, 변산반도, 오대산
cluster3: 무등산, 북한산, 설악산, 지리산, 한려해상
여기까지 파이썬 기반 K-평균 클러스터링으로 22개 국립공원을 육지면적, 탐방객수 특징에 따라 유형 분류해 봤습니다. 보다 완결성 있는 소스 코드는 원문을 작성한 개발자의 다음 깃허브주소를 참조하시기 바랍니다. 감사합니다.
pavankalyan1997/Machine-learning-without-any-libraries
This is a collection of some of the important machine learning algorithms which are implemented with out using any libraries. Libraries such as numpy and pandas are used to improve computational co...
github.com
