안녕하세요? 이번 글은 파이썬의 ESDA 패키지를 통한 '공간 자기상관(Spatial Autocorrelation)' 실습 과정을 정리해 보겠습니다. 이 글은 캐나다 Clearly에서 데이터 및 분석 리더로 활동하시는 Peng Wang(펭 왕) 님의 블로그 글을 번역, 정리 및 보완한 것입니다.
Exploratory Spatial Data Analysis (ESDA) – Spatial Autocorrelation – AI Journey
In exploratory data analysis (EDA), we often calculate correlation coefficients and present the result in a heatmap. Correlation coefficient measures the statistical relationship between two variables. The correlation value represents how the change in one
ai-journey.com
ESDA(탐색적 공간 데이터 분석)
아래는 '통계의 큰 그림(Big Picture of Statistics)'이라는 제목의 그림입니다. 통계는 크게 보면 관심 모집단에서 샘플 데이터를 수집하고, 수집한 데이터를 요약(summarizing)하고, 확률과 추론을 통해 샘플에서 수집된 데이터를 기반으로 전체 모집단에 대한 결론을 도출하는 단계로 볼 수 있습니다.
EDA(Exploratory Data Analysis, 탐색적 데이터 분석)는 데이터를 원시 형식에서 보다 유익한 형식으로 변환하여 이해하는 방법을 의미합니다. 기존의 EDA는 지리적 특징을 다른 일반 특징과 유사하게 처리하므로, 여기서는 공간 데이터의 탐색적 분석을 위한 ESDA(Exploratory Spatial Data Analysis, 탐색적 공간 데이터 분석)를 사용합니다.

ESDA는 공간 데이터의 탐색적 분석을 위한 오픈소스 Python 라이브러리입니다. PySAL(Python Spatial Analysis Library)의 하위 패키지로 광역적 공간 자기상관(Global Spatial Autocorrelation), 지역적 공간 자기상관 분석(Local Spatial Autocorrelation)을 모두 포함하고 있습니다. 간략한 개념 정리 후, ESDA로 공간 자기상관을 실습해 보겠습니다.
Exploratory Analysis of Spatial Data: Spatial Autocorrelation — esda v2.4.3 Manual
Exploratory Analysis of Spatial Data: Spatial Autocorrelation In this notebook we introduce methods of exploratory spatial data analysis that are intended to complement geovizualization through formal univariate and multivariate statistical tests for spati
pysal.org
상관(Correlation)
두 개의 변수가 어느 정도 규칙적으로 동시에 변화되어 가는 성질을 상관(correlation)이라 하며, 두 변수 간에 어떤 선형적 관계가 있는지 분석하는 방법을 상관 분석(correlation analysis)이라고 합니다. 선형성(linearity, 리니어리티)은 두 변수 X와 Y의 관계가 직선적인지를 알아보는 것으로 이 가정은 분포를 나타내는 산점도(scatter plot)를 통하여 확인할 수 있습니다. 상관 분석은 단순히 두 개의 변수가 어느 정도 강한 관계에 있는가를 측정하는 단순상관분석(simple correlation analysis)과, 2개 이상의 변수간 관계 강도를 측정하는 다중상관분석(multiple correlation analysis)이 있습니다.
두 변수 사이의 통계적 관계를 표현하기 위해 특정한 상관 관계의 정도를 수치적으로 나타낸 계수를 상관 계수(correlation coefficient)라고 합니다. 상관 계수 값의 범위는 -1에서 +1 사이에 속하며 여기서 ±1은 정도가 가장 센 잠재적 일치를, 0은 정도가 가장 센 불일치를 나타냅니다. 상관 계수는 두 변수간의 연관된 정도를 나타낼 뿐 인과관계를 설명하는 것은 아니므로 두 변수 간에 원인과 결과의 인과관계에 대한 것은 회귀분석(regression analysis)을 통해 확인해 볼 수 있습니다.
자기상관(Autocorrelation)
Auto-는 Self-(자기 자신의)라는 의미를 가지고 있습니다. 시간 또는 공간적으로 연속된 일련의 관측치들 간에 존재하는 상관관계를 자기상관(autocorrelation)이라고 합니다. 시계열 데이터에서 시계열 자기상관(temporal autocorelation)은 주어진 변수와 시간 이동된 자기 자신과의 상관관계를 측정합니다. 공간 데이터에서 공간적 자기상관(spatial autocorrelation)은 주어진 변수와 주어진 변수의 위치 사이의 상관관계를 측정합니다.
공간 자기상관(Spatial Autocorrelation)
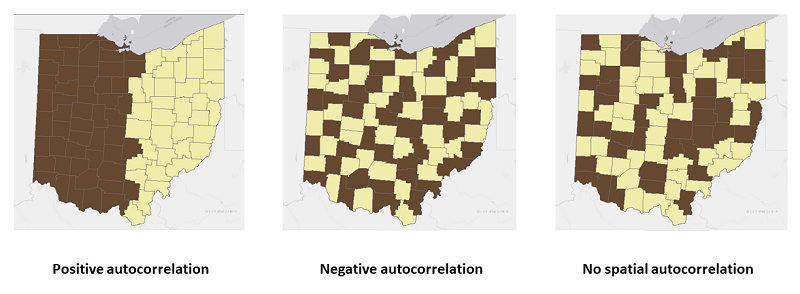
공간 자기상관(spatial autocorrelation)은 공간적 근접성(spatial proximity)으로 인한 하나의 속성 값 간의 종속성을 측정합니다. 공간 자기상관 측정은 세 가지 범주의 공간 패턴을 보여줍니다.
1) 유사한 값이 근처에 있음을 나타내는 양의 공간 자기상관 (Positive autocorrelation)
2) 서로 다른 값이 함께 있는 경향이 있음을 나타내는 음의 공간 자기상관 (Negative autocorrelation)
3) 제로 공간 자기상관 또는 무작위 분포: 인근 위치에서 유사하거나 유사하지 않은 값의 유의성이 없음 (No spatial autocorrelation)
인접성(Contiguity) 정의
공간 자기상관은 공간 유사성(spatial similarity)과 속성 유사성(attribute similarity)을 결합합니다. 공간 유사성은 인접성(contiguity: 칸터규어티) 기반 공간 가중치(spatial weight)로 측정하며 이웃 관계(neighborhood relations)를 Rook(루크), Bishop(비숍), Queen(퀸)의 경우로 정의합니다. 루크는 각 셀에 인접한 4개 위치의 이웃을, 비숍은 대각선만 고려하며 퀸은 8개 셀의 이웃을 고려합니다. 속성 유사성은 공간 시차(spatial lag)로 정의합니다.

실습 데이터
실습 데이터는 경상남도 진주시의 표준지공시지가정보와 법정구역정보를 사용하겠습니다. 표준지공시지가정보는 매년 1월 1일을 기준으로 표준지의 단위면적당 가격정보(원/㎡)를 제공합니다. 법정구역정보는 법정동의 경계구역을 표시한 정보입니다. 실습 목표는 진주시의 공시지가와 법정구역 위치 사이의 상관관계가 있는지 조사하는 것입니다.
실습은 Google Colab(구글 코랩)으로 진행해보겠습니다.
GitHub - osgeokr/ESDA
Contribute to osgeokr/ESDA development by creating an account on GitHub.
github.com
먼저 실습에 필요한 패키지를 설치합니다.
# 패키지 설치
!pip install geopandas -q
!pip install mapclassify -q
!pip install pysal -q플롯에 한글 폰트를 적용하기 위해 나눔고딕을 설치하겠습니다. 설치 후 런타임을 다시 시작해야 하므로 런타임 종료 코드를 포함시켰습니다.
# 나눔고딕 설치
!sudo apt-get install -y fonts-nanum
!sudo fc-cache -fv
!rm ~/.cache/matplotlib -rf
import os
os.kill(os.getpid(), 9) # 런타임 종료이제 실습에 필요한 패키지를 호출합니다.
# 패키지 호출
import pandas as pd
import geopandas as gpd
import folium
from google.colab import files
import matplotlib.pyplot as plt
plt.rc('font', family='NanumGothic')
import libpysal as lps
import esda
from splot.esda import plot_moran, moran_scatterplot, lisa_cluster
from esda.moran import Moran, Moran_Local진주시 표준지공시지가 데이터(*.csv 포맷)를 DataFrame으로 읽어옵니다.
# 진주시 표준지공시지가
data_df = pd.read_csv('https://raw.githubusercontent.com/osgeokr/ESDA/main/DATA/JINJU_PRICE.csv')
data_df.head()진주시 표준지공시지가 데이터를 DataFrame에서 GeoDataFrame으로 변환합니다.
# 진주시 표준지공시지가 GeoDataFrame
data_gdf = gpd.GeoDataFrame(data_df, geometry=gpd.points_from_xy(data_df.xcoord, data_df.ycoord), crs='EPSG:5179')
data_gdf.head()공시가격이 들어있는 컬럼은 'A9'입니다. 해당 속성값으로 진주시 공시지가를 플로팅해 보겠습니다.


총 5,237개 공시 가격을 제공하고 있습니다.
len(data_gdf)이번에는 진주시 법정구역정보(읍면동) 데이터(*.geojson)를 GeoDataFrame으로 읽어옵니다.
# 진주시 법정구역정보(읍면동) GeoDataFrame
nbr_gdf = gpd.read_file('https://raw.githubusercontent.com/osgeokr/ESDA/main/DATA/JINJU_ADM.geojson')
nbr_gdf.head()진주시 법정구역을 플로팅해 보겠습니다.
fig, ax = plt.subplots(figsize = (10,10))
nbr_gdf.plot(ax=ax)
ax.set_title('진주시 법정구역', fontsize=15, fontweight='bold')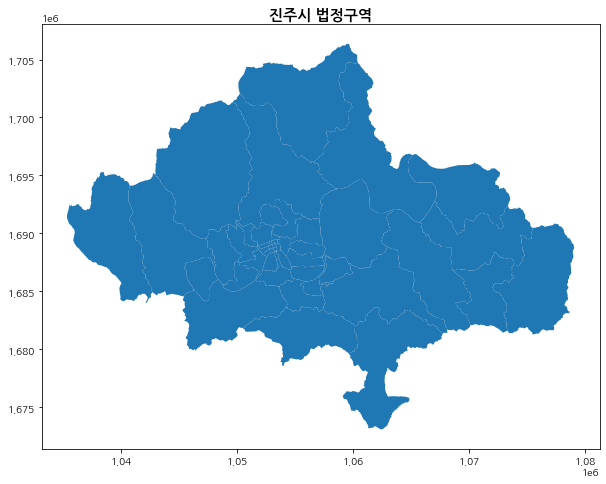
총 49개 법정구역을 제공하고 있습니다.
len(nbr_gdf)공간 조인(Spatial Join)
법정구역과 공시지가를 공간 조인(spatial join)해 보겠습니다.
# 공간 조인(Spatial Join)
prices = gpd.sjoin(nbr_gdf, data_gdf[['A9','geometry']], op='contains')
prices.head()법정구역은 총 5,223개 공시지가를 포함합니다.
len(prices)다음으로 법정구역별 평균 공시지가를 계산합니다.
pd.options.display.float_format = '{:.1f}'.format
# 법정구역별 평균 공시지가
nbr_avg_price = prices['A9'].groupby([prices['A2']]).mean()
nbr_final = nbr_gdf.merge(nbr_avg_price, on='A2')
nbr_final.rename(columns={'A2': 'adm'}, inplace=True)
nbr_final.rename(columns={'A9': 'avg_price'}, inplace=True)
nbr_final.head()49개 법정구역별 평균 공시지가가 계산되었습니다.
len(nbr_final)단계구분도(Choropleth: 코로플레스)
진주시 법정구역별 평균 공시지가를 단계구분도(Choropleth: 코로플레스)로 작성해 보겠습니다. 아래 코드는 최저가와 최고가를 5등분하여 인터렉티브 지도(*.html 포맷)로 표현한 것입니다.
# 단계구분도
m = folium.Map(location=[35.1847, 128.1131], zoom_start=11)
folium.TileLayer('CartoDB positron').add_to(m)
title = '진주시 법정구역별 평균 공시지가'
title_html = '''
<h3 align="center"><b>{}</b></h3>
'''.format(title)
m.get_root().html.add_child(folium.Element(title_html))
choropleth = folium.Choropleth(geo_data=nbr_final,
data=nbr_final,
bins=5, # 5단계
columns=['adm', 'avg_price'],
key_on='feature.properties.adm',
line_color='black',
line_width=1,
fill_color='YlOrRd',
fill_opacity=0.5,
line_opacity=0.5,
legend_name='평균 공시지가(원/㎡, 기준일: 2022.9.29.)'
).add_to(m)
choropleth.geojson.add_child(
folium.features.GeoJsonTooltip(['adm','avg_price'], labels=True, localize=True))
m.save('JINJU_ADM_AVG_PRICE.html')
files.download('JINJU_ADM_AVG_PRICE.html')
이번에는 진주시 법정구역별 평균 공시지가를 5분위수로 표현해 보겠습니다.
# 단계구분도(5분위수)
fig, ax = plt.subplots(figsize=(10,10))
nbr_final.plot(column='avg_price', scheme='Quantiles', k=5, cmap='GnBu', legend=True, ax=ax) # 분위수
nbr_final.boundary.plot(ax=ax)
plt.title('진주시 법정구역별 평균 공시지가', fontsize=15, fontweight='bold')
plt.tight_layout()
plt.show()
유사성(Similarity: 시밀러리티) 측정
두 가지 유형의 유사성, 공간 유사성과 속성 유사성을 측정합니다. 여기서는 퀸 인접성을 사용하여 공간 가중치와 공간 시차를 계산합니다. avg_price는 (평균) 공시지가를, weighted_price는 가중치 적용 (평균) 공시지가를 나타냅니다.
# 공간 유사성(Spatial similarity)
w = lps.weights.Queen.from_dataframe(nbr_final)
w.transform = 'r'
# 속성 유사성(Attribute similarity)
nbr_final['weighted_price'] = lps.weights.lag_spatial(w, nbr_final['avg_price'])
nbr_final.head()
공시지가와 가중치 적용 공시지가(공시지가의 공간 시차)를 비교한 플롯입니다.
f,ax = plt.subplots(1,2,figsize=(20,10))
nbr_final.plot(column='avg_price', scheme='Quantiles', k=5, cmap='GnBu', legend=True, ax=ax[0]) # 분위수
nbr_final.boundary.plot(ax=ax[0])
ax[0].set_title("공시지가", fontsize=15, fontweight='bold')
ax[0].axis('off')
nbr_final.plot(column='weighted_price', scheme='Quantiles', k=5, cmap='GnBu', legend=True, ax=ax[1]) # 분위수
nbr_final.boundary.plot(ax=ax[1])
ax[1].set_title("가중치 적용 공시지가", fontsize=15, fontweight='bold')
ax[1].axis('off')
plt.show()
광역적 공간 자기상관(Global Spatial Autocorrelation)
광역적 공간 자기상관을 계산해 보겠습니다. Moran의 I(Moran's I)값은 공간 자기상관을 측정하는 대표적인 방법입니다. Moran의 I값이 1에 가까울수록 공간 분포가 군집을 이룬다는 것을, -1에 가까울수록 공간 분포가 분산되어 있다는 것을 의미합니다. 그리고 0에 근접한 경우, 특정 공간 패턴이 나타나지 않은 무작위 공간 분포를 의미합니다. Moran의 I값은 통계적 유의성 검정을 통하여 통계가 유의한 값인지를 판단합니다.
확인 결과 Moran's I는 0.56, 유의확률 p-값은 0.001로 산출됩니다. 완전한 공간적 무작위성(complete spatial randomness)이라는 귀무가설이 기각되고 공간적인 패턴이 나타나는 대립가설이 채택됩니다.
# 광역적 공간 자기상관
y = nbr_final.avg_price
moran = esda.Moran(y, w)
moran.I, moran.p_sim # Moran의 I값, p-값plot_moran(moran, zstandard=True, figsize=(10,5))
plt.rcParams['axes.unicode_minus'] = False
plt.ylabel('가중 공시지가')
plt.xlabel('공시지가')
plt.tight_layout()
plt.show()
지역적 공간 자기상관(Local Spatial Autocorrelation)
광역적 공간 자기상관은 공간상에 존재하는 데이터 전체의 군집화 정도를 나타내며 진주시 공시지가는 행정구역에서 공간적인 패턴이 있다고 판단할 수 있습니다. 그러나 광역적 공간 자기상관으로는 공시지가가 어느 지역이 군집을 이루는지, 어느 지역이 주변지역의 경향과는 다른 패턴을 보이는 이상 지역인지, 혹은 관심 지역에 나타내는 지역적 군집이 어떤 종류를 가지는지에 대해서는 알 수 없습니다.
공시지가의 공간 군집이 어느 지역에서 나타나는지 파악하고 지역별로 서로 상이한 공간 패턴과 지가의 이상 지역을 발견하기 위해서는 지역적 공간 자기 상관 분석을 사용합니다. 지역적 공간 자기상관은 지역 공간 연관성 지표(LISA: Local Indicator of Spatial Association)를 측정합니다. LISA를 통해 추출된 공간 군집은 지역적 상관관계를 나타내는 High-High(HH), Low-Low(LL)와 지역적으로 주변 지역과 유사하지 않음을 나타내는 Low-High(LH), High-Low(HL)로 분류됩니다.
1) HH 군집: 본 지역의 변수가 높은 값을 가지면서 주변의 값 또한 높은 경향을 보임.
2) LL 군집: 본 지역의 변수가 낮은 값을 가지면서 주변의 값 또한 낮은 경향을 보임.
3) LH 군집: 본 지역의 변수가 낮은 값을 가지는 데 반하여 주변의 값은 높은 경향을 보임.
4) HL 군집: 본 지역의 변수가 높은 값을 가지는 데 반하여 주변의 값은 낮은 경향을 보임.
# 지역 공간 자기상관
moran_local = Moran_Local(y, w)
fig, ax = plt.subplots(figsize=(10,10))
moran_scatterplot(Moran_Local(y, w), p=0.05, ax=ax)
ax.set_xlabel('공시지가')
ax.set_ylabel('가중 공시지가')
plt.text(1.75, 0.50, 'HH', fontsize=25)
plt.text(1.75, -0.75, 'HL', fontsize=25)
plt.text(-0.75, 0.50, 'LH', fontsize=25)
plt.text(-0.75, -0.75, 'LL', fontsize=25)
plt.show()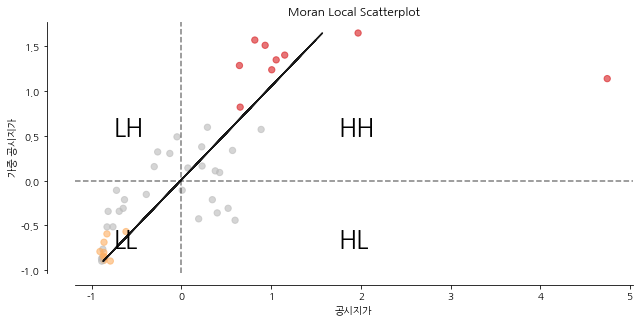
HH 군집의 경우 핫스팟(hot-spot)으로, LL 군집의 경우는 콜드 스팟(cold-spot)으로 볼 수 있으며, 두 경우는 주어진 변수가 공간적으로 양의 연관성을 갖습니다. LH 군집과 HL 군집은 이상 지역(outlier), 또는 고립지역으로 볼 수 있으며, 이 경우에는 공간적으로 음의 연관성을 가진다고 볼 수 있습니다.
LISA를 통해 진주시 법정구역별 가중 공시지가를 단계구분도로 표현한 결과입니다. 핫스팟과 콜드 스팟을 확인하실 수 있습니다.
fig, ax = plt.subplots(figsize=(10,10))
fig = lisa_cluster(moran_local, nbr_final, p=0.05, ax=ax)
nbr_final.boundary.plot(ax=ax)
plt.title('진주시 법정구역별 가중 공시지가 단계구분도', fontsize=15, fontweight='bold')
plt.tight_layout()
plt.show()
여기까지 파이썬의 ESDA 패키지를 통한 '공간 자기상관' 실습 과정을 정리해 봤습니다. 관련해서 Geographic Data Science with Python(https://geographicdata.science/book/intro.html) 오픈북 내용을 참고해 보시면 좋겠습니다. 저도 틈틈이 내용을 추가 정리해 보겠습니다.
