안녕하세요? 이번 글은 시리즈 글의 일부로 Google Earth Engine과 geemap을 이용한 종 분포 모델링(SDM: Species Distribution Modeling) 구현 방법을 소개해 보겠습니다. 이 글의 내용은 스미소니언 보전생물연구소 연구진 분들이 제공한 JavaScript 소스코드를 Python으로 변환하여 수정, 보완한 것입니다.
Crego, R. D., Stabach, J. A., & Connette, G. (2022). Implementation of species distribution models in Google Earth Engine. Diversity and Distributions, 28, 904–916. https://doi.org/10.1111/ddi.13491
사례 연구 1: 출현-전용 데이터를 이용한 팔색조(Pitta nympha) 서식지 적합성 및 예측 분포 모델링
8. 변수 중요도 계산
Random Forest(ee.Classifier.smileRandomForest)는 앙상블 학습 방법 중 하나로, 여러 개의 의사 결정 트리(decision tree)를 구성하여 예측을 수행하는 방법입니다. 각 의사 결정 트리는 데이터의 서로 다른 부분 집합을 기반으로 독립적으로 학습하며, 그 결과를 종합하여 더 정확하고 안정적인 예측을 가능하게 합니다.
변수 중요도(variable importance)란 Random Forest 모델 내에서 어떤 변수가 예측에 영향을 많이 미치는지를 평가하는 지표입니다. 앞서 정의된 SDM() 함수에서 ClassifierPr 변수는 확률 모드로 훈련된 Random Forest 분류기입니다. 이 변수를 추가 리턴해서 변수 중요도를 계산해 보겠습니다.
def SDM(x):
Seed = ee.Number(x)
# 훈련 및 검증을 위한 무작위 블록 분할
GRID = ee.FeatureCollection(Grid).randomColumn(seed=Seed).sort('random')
TrainingGrid = GRID.filter(ee.Filter.lt('random', split)) # 훈련용 격자
TestingGrid = GRID.filter(ee.Filter.gte('random', split)) # 시험용 격자
# 출현 지점
PresencePoints = ee.FeatureCollection(Data)
PresencePoints = PresencePoints.map(lambda feature: feature.set('PresAbs', 1))
TrPresencePoints = PresencePoints.filter(ee.Filter.bounds(TrainingGrid)) # 훈련용 출현 지점
TePresencePoints = PresencePoints.filter(ee.Filter.bounds(TestingGrid)) # 검증용 출현 지점
# 임의-비출현 지점
TrPseudoAbsPoints = AreaForPA.sample(region=TrainingGrid,
scale=GrainSize,
numPixels=TrPresencePoints.size().add(300),
seed=Seed,
geometries=True)
# 훈련용 출현 지점과 동일한 수의 임의-비출현 지점
TrPseudoAbsPoints = TrPseudoAbsPoints.randomColumn().sort('random').limit(ee.Number(TrPresencePoints.size()))
TrPseudoAbsPoints = TrPseudoAbsPoints.map(lambda feature: feature.set('PresAbs', 0))
TePseudoAbsPoints = AreaForPA.sample(region=TestingGrid,
scale=GrainSize,
numPixels=TePresencePoints.size().add(100),
seed=Seed,
geometries=True)
# 검증용 출현 지점과 동일한 수의 임의-비출현 지점
TePseudoAbsPoints = TePseudoAbsPoints.randomColumn().sort('random').limit(ee.Number(TePresencePoints.size()))
TePseudoAbsPoints = TePseudoAbsPoints.map(lambda feature: feature.set('PresAbs', 0))
# 훈련 및 임의-비출현 지점 병합
trainingPartition = TrPresencePoints.merge(TrPseudoAbsPoints) # 훈련용 지점
testingPartition = TePresencePoints.merge(TePseudoAbsPoints) # 시험용 지점
# 훈련용 지점에서 예측 변수 이미지의 공변량 값 추출
trainPixelVals = predictors.sampleRegions(collection=trainingPartition,
properties=['PresAbs'],
scale=GrainSize,
tileScale=16,
geometries=True)
# 랜덤 포레스트 분류기(Random Forest classifier)
Classifier = ee.Classifier.smileRandomForest(
numberOfTrees=500, # 생성할 결정 트리의 수
variablesPerSplit=None, # 분할당 변수의 수. 기본값: 변수 수의 제곱근 사용
minLeafPopulation=10, # 훈련 셋에 최소한 이 개수의 지점이 포함된 노드만 생성
bagFraction=0.5, # 트리당 백에 대한 입력 비율
maxNodes=None, # 각 트리의 최대 리프 노드 수. 기본값: 제한 없음
seed=Seed # 무작위화 시드
)
# 출현 확률(Presence probability)
ClassifierPr = Classifier.setOutputMode('PROBABILITY').train(trainPixelVals, 'PresAbs', bands)
ClassifiedImgPr = predictors.select(bands).classify(ClassifierPr)
# 이진 출현/비출현 지도(Binary presence/absence map)
ClassifierBin = Classifier.setOutputMode('CLASSIFICATION').train(trainPixelVals, 'PresAbs', bands)
ClassifiedImgBin = predictors.select(bands).classify(ClassifierBin)
# return ee.List([ClassifiedImgPr, ClassifiedImgBin, trainingPartition, testingPartition])
return [ClassifiedImgPr, ClassifiedImgBin, trainingPartition, testingPartition], ClassifierPr아래 코드에서 SDM() 함수는 10회 반복(numiter = 10)됩니다. ClassifierPr 변수로부터 각 반복별 변수 중요도 값을 리턴받아, 변수 중요도의 평균 값을 계산합니다. 이를 통해 각 변수의 상대적인 중요도, 즉 어떤 변수가 모델의 예측에 가장 큰 영향을 주는지를 알 수 있습니다.
split = 0.70 # 공간 블록은 모델 적합의 경우 70%, 모델 검증의 경우 30%로 각각 분할
numiter = 10 # 반복 횟수
# runif = lambda length: [random.randint(1, 1000) for _ in range(length)] # 시드
# results = ee.List(runif(numiter)).map(SDM).flatten()
results_list = [] # SDM 결과 리스트 초기화
importances_list = [] # 변수 중요도 리스트 초기화
for item in [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]:
result, trained = SDM(item)
# SDM 결과 리스트 누적
results_list.extend(result)
# 변수 중요도 리스트 누적
importance = ee.Dictionary(trained.explain()).get('importance')
importances_list.extend(importance.getInfo().items())
# SDM 결과 누적
results = ee.List(results_list).flatten()
# 각 변수 중요도 값을 리스트로 추출
variables = [item[0] for item in importances_list]
importances = [item[1] for item in importances_list]
# 변수 중요도 평균 계산
average_importances = {}
for variable in set(variables):
indices = [i for i, var in enumerate(variables) if var == variable]
average_importance = np.mean([importances[i] for i in indices])
average_importances[variable] = average_importance
# 평균 변수 중요도 출력
for variable, avg_importance in average_importances.items():
print(f"{variable}: {avg_importance}")elevation: 59.412175503770165
slope: 12.964208580184746
bio09: 17.23805871882852
aspect: 3.722224972595891
bio14: 6.250779258945053
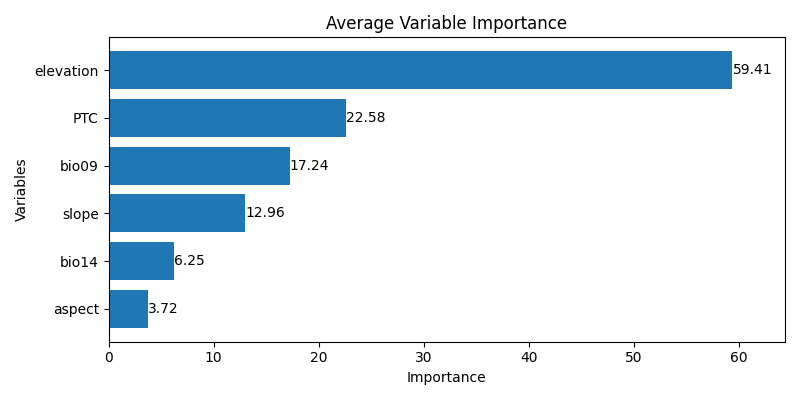
PTC: 22.578786069539074평균 변수 중요도를 시각화하여, 변수 중요도가 높은 순으로 정렬된 막대 그래프를 생성합니다. 각 막대 위에 해당 변수의 평균 중요도 값을 표시하여 변수 간의 상대적 중요도를 시각적으로 비교할 수 있습니다.
# 변수 중요도가 높은 순으로 정렬
sorted_importances = sorted(average_importances.items(), key=lambda x: x[1], reverse=False)
variables = [item[0] for item in sorted_importances]
avg_importances = [item[1] for item in sorted_importances]
# 그래프 크기 조절
plt.figure(figsize=(8, 4)) # 원하는 크기로 조절
# 막대그래프로 평균 중요도 출력
plt.barh(variables, avg_importances)
plt.xlabel('Importance')
plt.ylabel('Variables')
plt.title('Average Variable Importance')
# 막대 위에 수치 표시
for i, v in enumerate(avg_importances):
plt.text(v + 0.02, i, f"{v:.2f}", va='center')
# x축 범위 조정
plt.xlim(0, max(avg_importances) + 5) # 원하는 범위로 조절
plt.tight_layout()
plt.savefig('variable_importance.png')
plt.show()