안녕하세요? 이번 글은 기하학적인 관점에서 이미지 형성(image formation)을 설명한, LearnOpenCV 운영자 Satya Mallick(사티야 말릭) 님의 글을 일부 번역, 보완해 봤습니다. 특히, 3D의 한 점이 이미지 평면(image plane)에 투영되는 방법에 관한 수학을 다룰 것입니다.
Geometry of Image Formation
In this post, we will explain the image formation from a geometrical point of view. Specifically, we will cover the math behind how a point in 3D gets projected on the image plane. This post is written with beginners in mind but it is mathematical in natur
learnopencv.com
문제를 쉽게 이해하기 위해, 방에 카메라가 배치되어 있다고 가정해 보겠습니다. 이 방의 3D 점 P 가 주어지면 카메라로 촬영한 이미지에서 이 3D 점의 픽셀 좌표(u, v)를 찾고 싶습니다. 이 설정에는 세 가지 좌표계가 있습니다.
1. World Coordinate System(세계 좌표계)

그림 1: 세계 좌표계와 카메라 좌표계는 회전(Rotation)과 이동(translation)으로 연결됩니다. 이 6개의 매개변수(회전용 3개, 이동용 3개)를 카메라의 외부 파라미터(extrinsic parameters)라고 합니다.
방에 있는 점 위치를 정의하려면, 먼저 이 방에 대한 좌표계를 정의해야 합니다. 아래 두 가지가 필요합니다.
1. Origin(원점): 방의 모서리를 임의의 원점(0,0,0)으로 고정할 수 있습니다.
2. X, Y, Z축: 바닥의 2차원을 따라 방의 X와 Y축을 정의하고 또 수직벽을 따라 Z축을 정의할 수도 있습니다.
위 방법을 사용하여 X, Y, Z축을 따라 원점으로부터 거리를 측정하여 이 방에 있는 모든 점의 3D 좌표를 찾을 수 있습니다. 방에 연관된 이 좌표계를 World Coordinate System(세계 좌표계)이라고 합니다.
이 방의 점 P를 생각해 보겠습니다. 세계 좌표계에서 P 좌표는 (X_w, Y_w, Z_w)로 지정됩니다. 이 점의 X_w, Y_w, Z_w 좌표는 3개의 축을 따라 원점에서 이 점까지의 거리를 간단히 측정하여 찾을 수 있습니다.
2. Camera Coordinate System(카메라 좌표계)
이제, 이 방에 카메라를 설치해 보겠습니다.
방의 이미지는 이 카메라를 사용하여 캡처되므로, 이 카메라에 연관된 3D 좌표계가 중요합니다. 카메라를 방의 원점에 놓고 X, Y, Z 축이 방의 X_w, Y_w, Z_w 축과 정렬되도록 정렬했다면, 두 좌표계는 동일합니다.
그러나 이것은 비상식적인 제약입니다. 카메라를 방에 아무데나 놓고 그것은 어디에서나 볼 수 있어야 합니다. 이 경우, 3D 방(즉, 세계) 좌표계와 3D 카메라 좌표계 간의 관계를 찾아야 합니다.
카메라가 방의 임의의 위치(t_X, t_Y, t_Z)에 있다고 가정해 보겠습니다. 카메라 좌표는 세계 좌표에 대해 (t_X, t_Y, t_Z)로 이동(translated)할 수 있습니다.
카메라는 또한 임의의 방향을 보고 있을 수도 있습니다. 즉, 카메라가 세계 좌표계를 기준으로 회전(rotated)한다고 말할 수 있습니다.
3D의 회전(Rotation)은 세 가지 파라미터를 사용하여 캡처됩니다. 세 가지 파라미터를 Pitch(피치, X축을 중심으로 회전, 종축), Yaw(요, Y축을 중심으로 회전, 횡축), Roll(롤, Z축을 중심으로 회전, 수직축)로 생각할 수 있습니다.


그러나 회전(Rotation)을 3x3 행렬로 인코딩하는 수학적 조작이 편리한 경우가 많습니다. 이제 3×3 행렬에는 9개의 요소가 있으므로 9개의 파라미터가 있지만 회전에는 3개의 파라미터만 있다고 생각할 수 있습니다.
세계 좌표와 카메라 좌표는 회전 행렬(rotation matrix) R과 3요소 이동 벡터(translation vector) t로 연결됩니다. 이게 무슨 뜻일까요?
세계 좌표계에서 좌표값(X_w, Y_w, Z_w)을 가지고 있던 점 P가 카메라 좌표계에서 서로 다른 좌표값(X_c, Y_c, Z_c)을 갖게 됨을 의미합니다.
두 좌표 값은 다음 방정식으로 연결됩니다.

회전을 행렬로 나타내면 간단한 행렬 곱셈으로 회전을 수행할 수 있습니다. 때때로 위의 표현은 더 간결한 형태로 작성됩니다. 3x1 이동 벡터는 3x3 회전 행렬의 끝에 열로 추가되어 Extrinsic Matrix(외부 행렬)이라는 3x4 행렬을 얻습니다.

여기서, 외부 행렬 P는 다음과 같이 주어집니다.

동차 좌표(Homogeneous coordinates) : 데카르트 좌표(cartesian coordinates: 임의의 차원의 유클리드 공간을 나타내는 좌표계의 하나)에서 3D 점 (X, Y, Z)는 (X, Y, Z, 1)로 쓸 수 있습니다.
[다크 프로그래머 블로그 글 내용 중] 동차 좌표는 쉽게 말하면 (x, y)를 (x, y, 1)로 표현하는 것입니다. 좀더 일반적으로 말하면 임의의 0이 아닌 상수 w에 대해 (x, y)를 (wx, wy, w)로 표현하는 것입니다. 즉, 동차 좌표에서 스케일(scale)은 무시되며 (x, y)에 대한 동차 좌표 표현은 무한히 많이 존재하게 됩니다. 마찬가지로, 3차원의 경우에는 (X, Y, Z)를 (X, Y, Z, 1)이나 (wX, wY, wZ, w)로 표현합니다.
[영상 Geometry #2] Homogeneous Coordinates
(3D 비전 geometry 2번째 파트 homogeneous coordinates 입니다) 2. Homogeneous Coordinates 먼저, 들어가기 앞서 http://blog.daum.net/shksjy/229 글을 읽어보기를 추천합니다. Homogeneous Coordinate에 대한..
darkpgmr.tistory.com
보다 일반적으로, 데카르트 좌표에서 동차 좌표 (X, Y, Z, W)는 점 (X/W, Y/W, Z/W)과 같습니다. 동차 좌표를 사용하면 유한 숫자를 사용하여 무한 수량을 나타낼 수 있습니다. 예를 들어, 무한대의 점은 동차 좌표에서 (1, 1, 1, 0)으로 나타낼 수 있습니다. 세계 좌표계를 나타내기 위해 위 방정식에서 동차 좌표를 사용했음을 알 수 있습니다.
3. Image Coordinate System(이미지 좌표계)
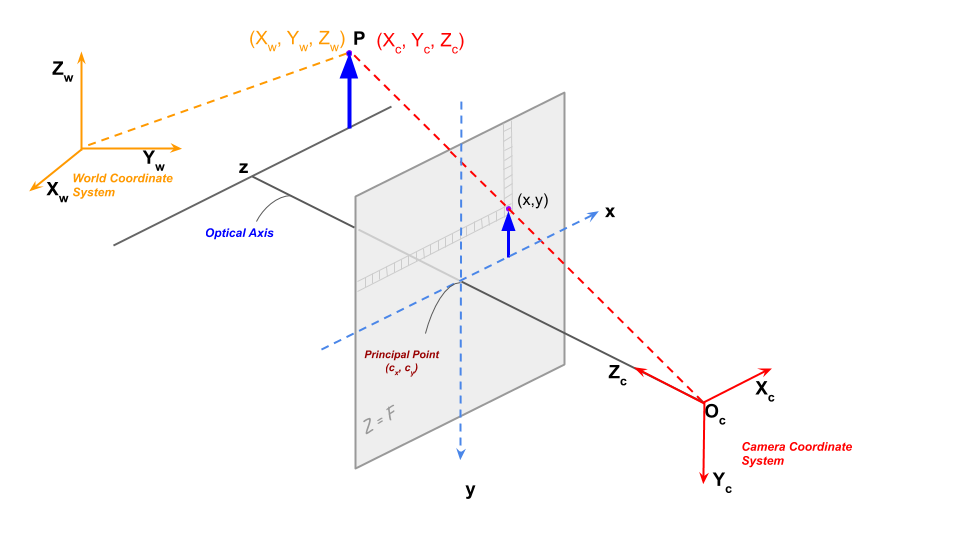
그림 2: 이미지 평면에 점 P의 투영이 표시됩니다.
점 세계 좌표에 회전 및 이동을 적용하여 카메라의 3D 좌표계에서 한 점을 얻으면, 이미지에서 점의 위치를 얻기 위해 이미지 평면에 점을 투영할 수 있는 위치에 있게 됩니다.
위 이미지에서 우리는 카메라 좌표계에서 좌표 (X_c, Y_c, Z_c)가 있는 점 P를 보고 있습니다. 이 점의 카메라 좌표계의 좌표를 모른다고 해도, 외부 행렬과 식을 사용하여 세계 좌표계를 변환하여 카메라 좌표계의 좌표를 얻을 수 있습니다.
그림 2는 단순 핀홀 카메라의 경우 카메라 투영을 보여줍니다. 광학 중심(핀 홀)은 O_c로 표현됩니다. 실제로는 점의 반전된 이미지가 이미지 평면에 형성됩니다. 센서에서 판독된 이미지는 반전을 되돌리기 위해 180도 쉽게 회전할 수 있으므로, 수학적 편의를 위해 이미지 평면이 광학 중심 앞에 있는 것처럼 모든 계산을 수행합니다. 실제로는 이마저도 필요하지 않습니다.
이미지 평면은 광학 중심에서 거리 f(초점거리)에 배치됩니다. 고등학교 기하학(닮은 삼각형)을 사용하여 3D 점 (Xc, Yc, Zc)의 프로젝트 이미지 (x, y)를 표시할 수 있습니다.
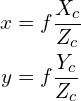
위 방정식들은 다음과 같은 행렬 형식으로 다시 작성할 수 있습니다.

아래 표시된 행렬 K는 Intrinsic Matrix(내부 행렬)이라고 하며 카메라의 내부 파라미터를 포함합니다.

위의 단순 행렬은 초점 거리만을 보여줍니다. 그러나 이미지 센서의 픽셀은 정사각형이 아닐 수 있으므로, 두 가지 다른 초점 거리 f_x와 f_y를 가질 수 있습니다. 카메라의 광학 중심 (c_x, c_y)는 이미지 좌표계의 중심과 일치하지 않을 수 있습니다. 또한, 카메라 센서의 x와 y축 사이에 약간의 기울기 γ(gamma)가 있을 수 있습니다.
위의 모든 사항을 고려한다면, 카메라 행렬은 다시 다음과 같이 다시 작성할 수 있습니다.


그림 3: 이미지 픽셀 좌표계가 왼쪽 상단 코너에 원점이 있는 경우 보다 현실적인 시나리오를 보여줍니다. 내부 카메라 행렬은 주점의 위치, 축의 기울기, 다른 축을 따라 잠재적으로 다른 초점 거리를 고려해야 합니다.
위의 식에서 x와 y 픽셀 좌표는 이미지의 중심을 기준으로 합니다. 그러나 이미지로 작업하는 동안 원점은 이미지의 왼쪽 상단 코너에 있습니다.
이미지 좌표를 (u, v)로 표현해 봅시다.


요약
카메라 픽셀 좌표에 세계 좌표계의 3D 점을 투영하는 것은 두 단계로 수행됩니다.
1. 3D 포인트는 두 좌표계 간의 회전 및 변환으로 구성된 외부 행렬을 사용하여 세계 좌표에서 카메라 좌표로 변환됩니다.
2. 카메라 좌표계의 새로운 3D 점은 초점 거리, 광학 중심 등과 같은 내부 카메라 파라미터로 구성된 내부 행렬을 사용하여 이미지 평면에 투영 됩니다.
